Home Searching Lesson
Post
Cancel

Searching Lesson

Posted Apr 23, 2024
By David Vasilev
13 min read

7.5 Searching

What does college board want you to know

  • Differences in searching using arrayList and arrays
  • Types of searches: sequential (linear) and binary
  • Searching for a double vs int vs object


Differences Reminder

  • Answer all the question, they are popcorn hacks

Arrays

  • Query looks like array[index]
  • array.length
  • int[] array = new int[];

arrayList

  • Query looks like arrayList.get(index)
  • arrayList.size()
  • ArrayList<Integer> arrayList = new ArrayList<Integer>();

Question 1

question1

1
2
3
4
5

for (int index = items.length - 1; index >= 0; index --) {
    if (items[index] == num) {
        return index;
    }
}

Question 2

question2

1
2
3
4
5

for (int index = 0; index < items.size(); index ++) {
    if (items.get(index) == num) {
        return index;
    }
}

Searching for a double vs int vs object

  1. Data Type Basics:
    • double is used for decimal numbers (like 3.14 or 10.5).
    • int is for whole numbers (like 5 or -10).
    • Object is a generic type that can hold any kind of data.
  2. Comparing Values:
    • With double and int, searching algorithms can directly compare values using simple checks like “Is this number greater than that number?”
    • With Object, the comparison might involve more steps, like checking specific properties of the objects.
  3. Performance Considerations:
    • double and int use less memory and have simpler comparison logic, which can make searching faster.
    • Object might be slower due to the need for more complex comparison logic and potentially larger memory usage.
  4. Handling Null Values:
    • With Object, you need to handle cases where the data is null (empty) to avoid errors during searching.
  5. Binary Search Advantage:
    • Binary search works best on sorted data, and with double and int, the sorting and comparison are straightforward.
    • With Object, sorting and comparison might require more effort, especially for custom data types.

gif

Linear or Sequential Search is a simple searching algorithm that checks each element in a list one by one until it finds a match or reaches the end of the list.

  • usually used when there is no specific order or structure to the data
  • O(n), where n is the number of elements in the array

Return the position of key in arr or -1 if key is not in arr.

Return true if key is in arr; otherwise, return false.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import java.util.ArrayList;

public class LinearSearch {

    // Iterative implementation for ArrayList<String>
    public static int iterativeLinearSearch(ArrayList<String> list, String target) {
        // Start from the first element of the list
        for (int i = 0; i < list.size(); i++) {

            // Compare each element with the target element until a match is found or the end of the list is reached
            if (list.get(i).equals(target)) {
                return i; // Element found at index i
            }
        }
        return -1; // Element not found
    }

    // Recursive implementation for ArrayList<String>
    private static int search(ArrayList<String> list, String target, int startIndex) {
        // Check if the startIndex is greater than or equal to the size of the list
        if (startIndex >= list.size())
            // If startIndex is out of bounds, return -1 -> target not found
            return -1;
    
        // Check if the string at the startIndex position in the list is equal to the target string
        if (list.get(startIndex).equals(target))
            // If the target string is found at startIndex, return the index
            return startIndex;
    
        // If the target string is not found at startIndex, recursively call the search method
        // with the incremented startIndex to continue searching in the rest of the list
        return search(list, target, startIndex + 1);
    }


    public static void example1(String[] args) {
        ArrayList<String> namesList = new ArrayList<>(Arrays.asList("Grace", "Emma", "Finn", "Theo", "Rachit", "Tanisha", "Vivian", "Aliya", "Justin"));

        int index = LinearSearch.iterativeLinearSearch(namesList, "Emma");
        if (index != -1) {
            System.out.println("Element found at index: " + index);
        } else {
            System.out.println("Element not found");
        }
    }

    public static void example2(String[] args) {
        ArrayList<String> namesList = new ArrayList<>(Arrays.asList("Grace", "Emma", "Finn", "Theo", "Rachit", "Tanisha", "Vivian", "Aliya", "Justin"));

        int index = LinearSearch.recursiveLinearSearch(namesList, "Vivian");
        if (index != -1) {
            System.out.println("Element found at index: " + index);
        } else {
            System.out.println("Element not found");
        }
    }
}


1
2

// Example with Iterative Implementation
LinearSearch.example1(null);

1

Element found at index: 1

1
2

// Example with Recursive Implementation
LinearSearch.example2(null);

1

Element found at index: 6

Popcorn Hack

  1. Implement linear search for an array list of integers
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import java.util.ArrayList;

public class LinearSearch {

    public static int linearSearch(ArrayList<Integer> arr, int target) {
        for (int i = 0; i < arr.size(); i++) {
            if (arr.get(i) == target) { // searching for specific element
                return i;
            }
        }
        return -1; // no element found
    }

    public static void main(String[] args) {
        ArrayList<Integer> list = new ArrayList<>();
        list.add(10);
        list.add(20);
        list.add(30);
        list.add(40);
        list.add(50);

        int target = 30;
        int index = linearSearch(list, target);

        if (index != -1) {
            System.out.println("Element " + target + " found at index " + index);
        } else {
            System.out.println("Element " + target + " not found");
        }
    }
}

LinearSearch.main(null);

1

Element 30 found at index 2
  1. When is it preferred to use linear search over binary search?

You would use linear when there are a small amount of elements (time complexity is better).

Recursive algorithms

  • a method that calls upon itself
  • has a “base case” that is a conditional statement that skips the recursive call so algorithm stops at certain point

recursive

  • useful when solving problems that can be broken down into smaller, repetitive problems

Popcorn Hack

What are some examples of algorithms that would be useful to have recursion?

  • Merge Sort, Quick Sort, Fib, Heap Sort

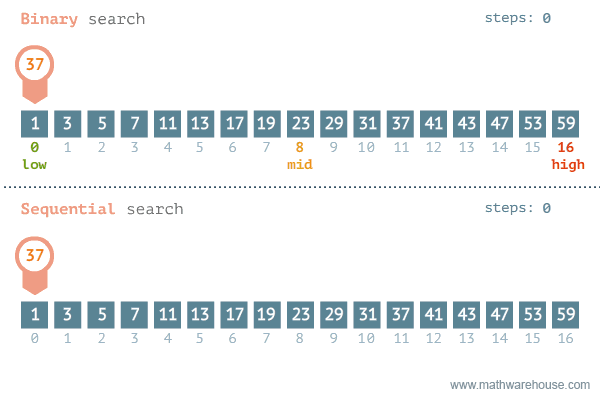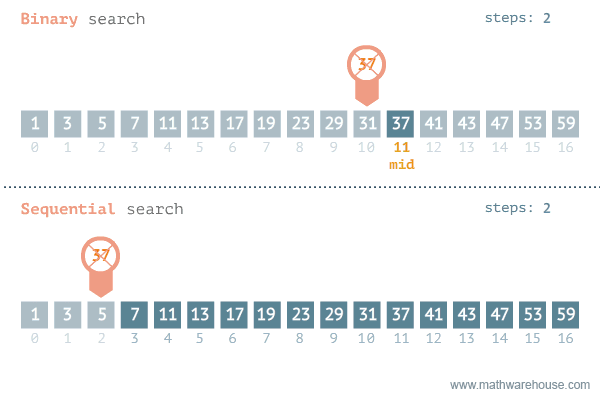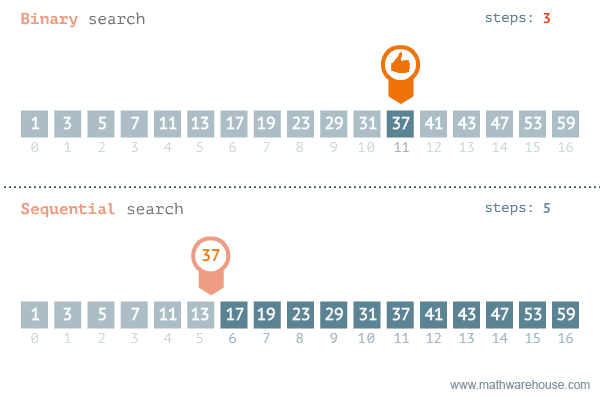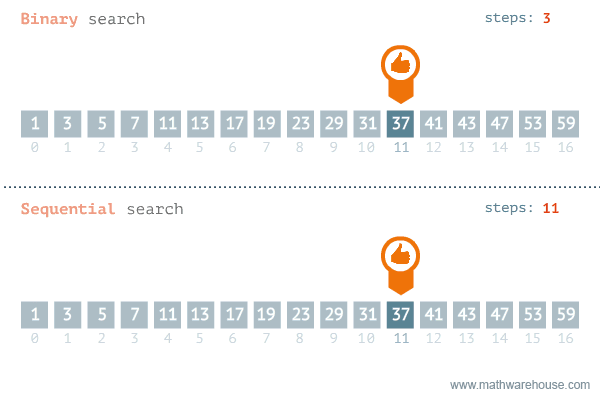
Binary Search

  • finds the index of an element of a SORTED array
  • why use it? can be faster than linear search which has O(n) complexity while binary has O(log N)
  • how it works simply: (Divide and Conquer method 💪)

  1. Start in the middle –> see if that number is lower or higher than the desired number

    a. if lower than disregard upper half section and only look at lower section

    b. if higher than disregard lower half and only look at upper section

  2. Find middle of that lower/higher section (those sections don’t include the original middle number)

    a. if even number of numbers in that section, you can specify in algorithm whether want to use lower or higher number

  3. Keep repeating process until find number

    a. if desired number trying to find is not in the list → high and low are swapped incorrectly → return -1

Simple example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

public class BinarySearch {
    static char[] arr = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'};

    public static String findMe(char target, int start, int end) {
        if (start > end) {
            return "Not Found";
        }

        // find middle number - java integer division automatically truncates
        int middle = (start + end) / 2;

        if (arr[middle] == target) {
            return "Found it at index " + middle;
        }

        // recursion spotted - search lower section
        if (arr[middle] > target) {
            return findMe(target, start, middle - 1);
        } 

        // recursion spotted part 2 - search higher section
        if (arr[middle] < target) {
            return findMe(target, middle + 1, end);
        }
        
        return "Not Found";
    }

    public static void main(String[] args) {
        char target = 'f';
        int start = 0;
        int end = arr.length - 1;
        System.out.println(findMe(target, start, end));
    }
}
BinarySearch.main(null);

1

Found it at index 5

Popcorn Hack

What iteration did it find f?

iteration 3

Hashmap searching

Introduction to HashMap:

  1. HashMap is a data structure that stores key-value pairs.
  2. Keys are hashed to determine their storage location in the map.
  3. Java’s HashMap provides O(1) time complexity for get() and put() operations.
  4. No keys can be the same, or else the old data is lost, and is replaced by the new one
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import java.util.HashMap;

public class HashMapSearching {
    public static void main(String[] args) {
        // Create a HashMap of students and their scores
        // Declaring the HashMap with <String, Integer> type
        HashMap<String, Integer> scores = new HashMap<>();
        scores.put("Alice", 85);
        scores.put("Bob", 90);
        scores.put("Charlie", 95);
        scores.put("Alice", 80);

        // Search for a student
        String name = "Alice";

        // containsKey() method is used to check if the key is present in the HashMap
        if (scores.containsKey(name)) {
            int score = scores.get(name);
            System.out.println(name + "'s score is: " + score);
        } else {
            System.out.println(name + " not found in the records.");
        }
    }
}

HashMapSearching.main(null);


1

Alice's score is: 80

Hashmaps with objects

  • What is an Abstract Class Review
    • Abstract classes can’t be made into objects
    • They enforce a structure for the subclasses generated by it

Hacks for this part

  1. Create a method to delete data based off the key
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

import java.util.HashMap;

public abstract class Collectable implements Comparable <Collectable> {
	public final String masterType = "Collectable";
	private String type;	// extender should define their data type

	// enumerated interface
	public interface KeyTypes {
		String name();
	}
    
	protected abstract KeyTypes getKey();  	// this method helps force usage of KeyTypes

	// getter
	public String getMasterType() {
		return masterType;
	}

	// getter
	public String getType() {
		return type;
	}

	// setter
	public void setType(String type) {
		this.type = type;
	}
	
	// this method is used to establish key order
	public abstract String toString();

	// this method is used to compare toString of objects
	public int compareTo(Collectable obj) {
		return this.toString().compareTo(obj.toString());
	}

	// static print method used by extended classes
	public static void print(Collectable[] objs) {
		// print 'Object' properties
		System.out.println(objs.getClass() + " " + objs.length);

		// print 'Collectable' properties
		if (objs.length > 0) {
			Collectable obj = objs[0];	// Look at properties of 1st element
			System.out.println(
					obj.getMasterType() + ": " + 
					obj.getType() +
					" listed by " +
					obj.getKey());
		}

		// print "Collectable: Objects'
		for(Object o : objs)	// observe that type is Opaque
			System.out.println(o);

		System.out.println();
	}
}

public class Car extends Collectable {
    private String make;
    private String model;
    private int year;

    public Car(String make, String model, int year) {
        this.make = make;
        this.model = model;
        this.year = year;
    }

	@Override
    protected KeyTypes getKey() {
        return null; 
    }

    public String getMake() {
        return make;
    }

    public String getModel() {
        return model;
    }

    public int getYear() {
        return year;
    }

    public String toString() {
        return year + " " + make + " " + model;
    }
}

public class Garage {
    private HashMap<String, Car> garage = new HashMap<>();

    public Garage() {
        garage.put("Lambo", new Car("Lamborghini", "Aventador", 2021));
        garage.put("Ferrari", new Car("Ferrari", "F8 Tributo", 2021));
        garage.put("Porsche", new Car("Porsche", "911 Turbo S", 2021));
        garage.put("McLaren", new Car("McLaren", "720S", 2021));
    }

    public void printGarage() {
        for (String key : garage.keySet()) {
            System.out.println(key + ": " + garage.get(key));
        }
    }

    public void deleteCarByKey(String key) {
        Car removedCar = garage.remove(key);
        if (removedCar == null) {
            System.out.println(key + " not found in the garage.");
        } else {
            System.out.println("Removed: " + key + ", " + removedCar);
        }
    }

    public static void main(String[] args) {
        Garage myGarage = new Garage();
        myGarage.printGarage();

        myGarage.deleteCarByKey("Lambo");
        myGarage.printGarage();
    }
}

Garage.main(null);

1
2
3
4
5
6
7
8

Ferrari: 2021 Ferrari F8 Tributo
Porsche: 2021 Porsche 911 Turbo S
Lambo: 2021 Lamborghini Aventador
McLaren: 2021 McLaren 720S
Removed: Lambo, 2021 Lamborghini Aventador
Ferrari: 2021 Ferrari F8 Tributo
Porsche: 2021 Porsche 911 Turbo S
McLaren: 2021 McLaren 720S

HACKS (you should be able to do with chatgpt)

  1. Is sequential/linear or binary more efficient? Why?

Binary search is more efficient for large data sets because of it’s time complexity. This is because the it works on the basis of dividing, narrowing down the answer more quickly than something like linear search.

  1. Why might you not always be able to use binary search?

Binary search can’t be used when the elements in the array are not sorted.

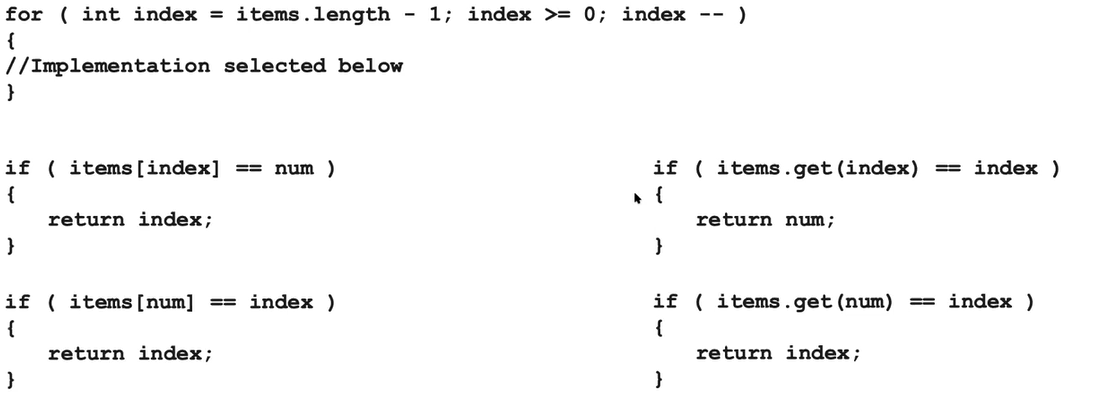
  1. Which of the following implements a method named contains for searching an array sequentially, confirming whether or not the array contains a requested element?

4 would be correct because all other implementations don’t work. 1 has a weird implementation, 2 only checks the final value in the array, and 3 immediately returns false and ends if the target is not found in the first place.

Answer the comment in the code

public static int foo(int[] arr, int x) {

1
2
3
4
5
6
7
8
9
10
11

for(int i = 0; i < arr.length; i++) {

    if(arr[i] == x) {

        return i;

    }

}

return -1;

}

Given the method defined above, how many times is the word “Indubitably!” output by the code below?

int[] vals = {1,4,51,3,14,91,130,14};

for(int i = 0; i < 20; i++) {

1
2
3
4
5

if(foo(vals,i%4) < 0) {

    System.out.println("Indubitably!");

}

}

Answer:

it would be outputted 3 times.

Lab Notebook
Java
This post is licensed under CC BY 4.0 by the author.
Contents

Workshop 4 - Lesson on 2D Arrays and Traversing them

Unit 7 Lesson